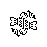
Before the discovery of the spacefiller, the fastest growth rates were attained using some variation of the breeder, which achieves quadratic growth by "breeding" linear-growth patterns such as glider guns at a linear rate. The classic breeder was the first example of such a pattern. A much smaller breeder has since been designed, and variations on this theme have been developed, such as the rake gun and the switch engine puffer.
Like the breeder, the spacefiller grows at a quadratic rate, which is easily seen to be the fastest attainable. However, the constant factor is much higher for the spacefiller. In addition, the spacefiller represents a conceptual leap in that it tiles the plane with a regular, stable pattern rather than a collection of discrete objects.
It is interesting to try to determine just how large a Life pattern needs to be before it can exhibit an explosive, quadratic rate of growth. The first spacefillers were already much smaller than any known breeders. Tim Coe has recently refined the known size bounds, and developed new spacefillers with other properties as well.
During the course of my searches for various types of space ships I ran across a fair number of c/2 ships that could act as spacefiller stretchers. Here are some of the resulting spacefillers I have managed to construct:
A 187 point spacefiller that fits in a 27 by 27 box.
A 189 point 2 cycle predecessor to David Bell's 206 point construction.
A 187 point rotationally symmetric spacefiller with flipper stretchers in place of the normally period 2 stretchers. The pattern on the interior of this spacefiller is forced by the stabilization requirements. This spacefiller also exists in a vertically reflected symmetric form that also has 187 points.
A ~194 point spacefiller with all flipper stretchers. A couple of the escort spaceships have been exploded to get some additional point reduction :-)
-Tim Coe
Back to Paul's Page of Conway's Life Miscellany